
J., “ Minimum-Fuel Low-Thrust Transfers for Spacecraft: A Convex Approach,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 54, No. 5, 2018, pp. 2274–2290. and Bennani S., “ Guidance of Reusable Launchers: Improving Descent and Landing Performance,” Journal of Guidance, Control, and Dynamics, Vol. 42, No. 10, 2019, pp. 2206–2219. and Pan B., “ Survey of convex Optimization for Aerospace Applications,” Astrodynamics, Vol. 1, No. 1, 2017, pp. 23–40. Lu P., “ Introducing Computational Guidance and Control,” Journal of Guidance, Control, and Dynamics, Vol. 40, No. 2, 2017, p. 193. T., “ Convex Relaxation for Optimal Rendezvous of Unmanned Aerial and Ground Vehicles,” Aerospace Science and Technology, Vol. 99, April 2020, Paper 105756. and Tang S., “ Adaptive Trajectory Generation Based on Real-Time Estimated Parameters for Impaired Aircraft Landing,” International Journal of Systems Science, Vol. 50, No. 15, 2019, pp. 2733–2751. and Holzapfel F., “ Optimal Rendezvous Guidance Laws with Application to Civil Autonomous Aerial Refueling,” Journal of Guidance, Control, and Dynamics, Vol. 41, No. 5, 2018, pp. 1167–1174. Wang Z., “ Optimal Trajectories and Normal Load Analysis of Hypersonic Glide Vehicles via Convex Optimization,” Aerospace Science and Technology, Vol. 87, April 2019, pp. 357–368.
J., “ Constrained trajectory Optimization for Planetary Entry via Sequential Convex Programming,” Journal of Guidance, Control, and Dynamics, Vol. 40, No. 10, 2017, pp. 2603–2615. and Padhi R., “ Robust Reentry Guidance of a Reusable Launch Vehicle Using Model Predictive Static Programming,” Journal of Guidance, Control, and Dynamics, Vol. 37, No. 1, 2014, pp. 134–148. and Xia Y., “ A Review of Optimization Techniques in Spacecraft Flight Trajectory Design,” Progress in Aerospace Sciences, Vol. 109, Aug. and Acikmese B., “ Successive Convexification for Mars 6-DoF Powered Descent Landing Guidance,” AIAA Guidance, Navigation, and Control Conference, AIAA Paper 2017-1500, 2017. S., “ An Optimal Guidance Law for Planetary Landing,” Guidance, Navigation, and Control Conference, AIAA Paper 1997-3709, 1997. and Shima T., “ Nonlinear Optimal Guidance for Intercepting a Stationary Target,” Journal of Guidance, Control, and Dynamics, Vol. 42, No. 11, 2019, pp. 2418–2431. and Holzapfel F., “ Generalized Impact Time and Angle Control via Look-Angle Shaping,” Journal of Guidance, Control, and Dynamics, Vol. 42, No. 3, 2019, pp. 695–702. and Holzapfel F., “ Polynomial Shaping of the Look Angle for Impact-Time Control,” Journal of Guidance, Control, and Dynamics, Vol. 40, No. 10, 2017, pp. 2668–2673. "iterations": The number of iterations taken.Liberzon D., Calculus of Variations and Optimal Control Theory: A Concise Introduction, Princeton Univ."algorithm": The algorithm used ( "nnls").

(The algorithm is stable and will converge given enough iterations.) output 0 indicates that the iteration count was exceeded, and therefore convergence was not reached >0 indicates that the algorithm converged.
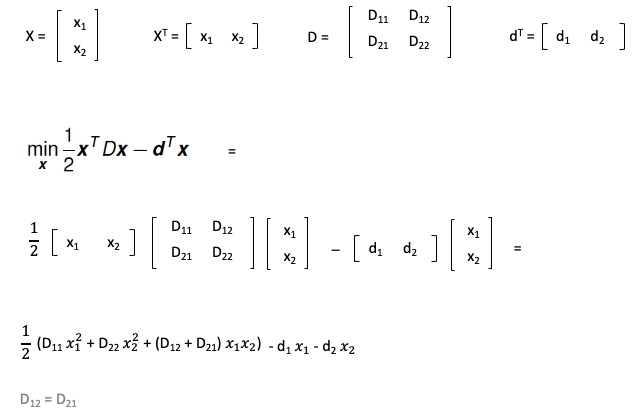
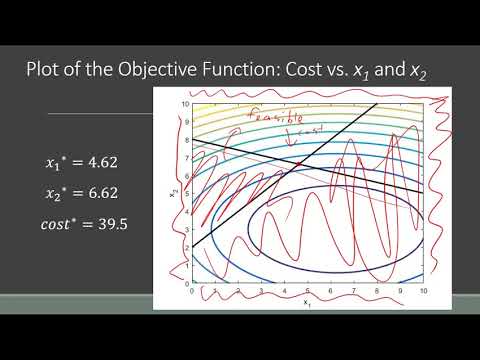
The minimum attained model value, 1/2* xmin'* c* xmin + d'* xmin exitflagĪn indicator of convergence. pqpnonneg recognizes one option: "MaxIter". Options is an options structure to change the behavior of the algorithm (see optimset).

X0 is an optional initial guess for the solution x. Octave can also solve Quadratic Programming problems, this is min 0.5 x'*H*x + x'*qĬ and d must be real matrices, and c must be symmetric and positive definite.


 0 kommentar(er)
0 kommentar(er)
